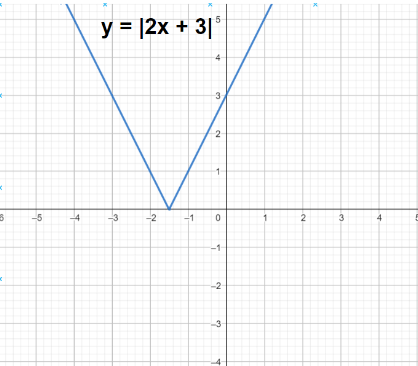Overview
Absolute value equations and functions are absolutely easy to master! Let’s do it right away!!
The distance of a number from 0 on the number line is its absolute value. It is denoted with a double vertical bar, with the number written inside it. As distance can’t be negative, an absolute value is never negative.
|5| = 5
|12| = 12
|-8| = 8
|-15| = 15
|0| = 0
As you can see, for a non-negative number, its absolute value is the same as the number itself.
For a negative number, the sign flips (negative becomes positive) and that’s it! Does this even have any use in real life? It does, we will show you later in the article. But first, make sure you understand the concept and can solve problems.
So, technically we can define the absolute value in the following way:
If x ≥ 0, |x| = x
If x < 0, |x| = -x
This is called a piecewise function, as the domain is broken up into pieces. The output, y, depends on which piece of the input x we are looking at.
Solving absolute value equations
The easiest way to solve an absolute value equation is to break it down into two parts – one positive and the other negative. Let’s take an example.
Solve for x:
|2x + 5| = 17
Solution:
Ignore the ‘2x + 5’. If the absolute value of something is 17, it can mean two things:
Either that ‘something’ equals 17 or that something equals -17.
So we have,
Either 2x + 5 = 17, in which case x = 6
Or 2x + 5 = -17, in which case x = -11
This is as good as solving two separate linear equations.
Solving absolute value inequalities
Solving absolute value inequalities is similar to solving absolute value equations.
Solve:
|x + 5| ≥ 3
Solution:
Just as in the previous example, ‘x + 5’ is not the key here. It could have been anything. The point is, the distance of some number is more than (or equal to) 3 from 0.
Once again, this can mean two things:
Either that ‘some number’ is larger than or equal to 3 or that some number is smaller than or equal to -3. These are the only two ways in which its distance from 0 can be more than or equal to 3.
So, we have
Either x + 5 ≥ 3, which means x ≥ -2
Or, x + 5 ≤ -3, which means x ≤ -8
Makes sense? Now, let’s take a quick look at how to graph an absolute value function.
Graphing absolute value functions
Being able to graph any absolute value function is a key skill that you will need to master in your HSC year 11 advanced maths curriculum.
Think about the parent absolute value function.
y = x if x ≥ 0
y = -x if x < 0
This means we need to split the graph into two parts – the region where x ≥ 0 and the region where x < 0
- In the region where x ≥ 0 we draw the graph of y = x
- In the region where x < 0 we draw the graph of y = -x, as shown below.
This is the “V-shape” you will get to hear about a lot over the next 2 years!
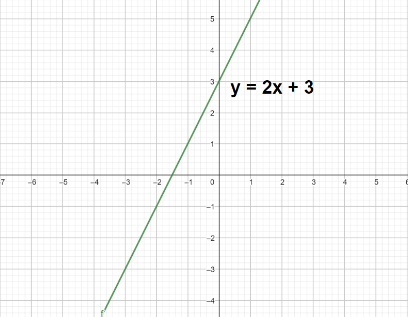
What about the graph of y = |2x + 3|? Any thoughts? Look, there are 2 ways to do this.
- Either you can use your knowledge on transformations – draw the graph of |x|, then use it to draw the graph of |2x| and then use that to draw the graph of |2x+3|
- Draw the graph of 2x + 3 – it’s a straight line with slope = 2 and y-intercept = 3
Now reflect the part that’s below the x-axis on the other side. You will do this because the absolute value is never negative, so the y-values that were negative become positive by the same amount.
In general, if you know what the graph of y = f(x) looks like, you should follow the same strategy – pretend the x-axis is a mirror and reflect the part of the graph that lies below it – to obtain the graph of y = |f(x)|.
Application
Are you still wondering how this could be applied in real life?
Imagine you are a meteorologist. You have access to a computer database that has the daily average temperatures in Sydney recorded over a period of 5 years. You found that the mean daily average temperature in Sydney over the 5 years is 20°C.
You want to find out, on what dates (over that period), Sydney witnessed an extreme climate. By ‘extreme climate’ you mean, the daily average was more than 8°C away from the normal temperature, which is 20°C.
If that sounds complicated, all it means is, you want to find out those dates when the daily average temperature was either less than 12°C (20 – 8) or more than 28°C (20 + 8). Makes sense?
Your computer doesn’t understand what you need unless you feed in a mathematical formula or an equation. You will want it to solve the inequality |x – 20| > 8
So that’s all about absolute values – in a nutshell – that you will learn in the HSC year 11 advanced maths curriculum. Once you understand the concepts, you should get some practice. Try out some challenging questions to test your understanding.
Feel free to contact us today, and we can give you a lot of practice on absolute value equations and functions.