All About Year 11 HSC Advanced Maths

How much tutoring
does your child need?

Overview

So, you are in year 11 and you want to find out what topics are covered in the HSC Advanced Maths curriculum, right?

 

By the time you finish reading this guide, you will have an overall idea of what the HSC Year 11 Advanced Maths syllabus covers. We will also share a couple of study tips that you might find helpful.

 

Let’s start with the syllabus….

 

HSC Year 11 Mathematics Syllabus (Advanced)

The year 11 specialist (advanced) Maths syllabus can be broadly classified into the following core topics:

1. Functions
2. Trigonometric Functions
3. Calculus
4. Exponential and Logarithmic Functions
5. Statistical Analysis

Let’s have a bird’s eye view of each one of these topics.

 

Functions

We bet you already have a fair bit of an idea on the concept of functions – at least linear functions. Remember y = mx + c? That’s a linear relationship between the independent variable (x) and the dependent variable (y).

 

You can think of a function as a mathematical rule relating two variables that can be plotted on the x-y coordinate plane. The independent variable is the ‘input’ and the dependent variable is the ‘output’. The rule applies to the input to produce the output.

A relationship (a table or a graph) represents a function only if each value of x corresponds to exactly one value of y. You can test this on the graph using the vertical line test. If you draw a vertical line at any point of your choice on the graph, for it to be a function, the line must not cross the graph at more than one point.

 

Then you have domains and ranges – the allowed values for the inputs and the outputs, respectively. “Allowed values?” What’s not allowed? Let me explain…

 

Think about the function \(y=\sqrt{x}.\) In plain English, this means “the output is the square root of the input”. Ok, then what’s the output when the input is a negative number? Nothing, right? It doesn’t exist. So, you are not allowed to input a negative number into this function. In other words, its domain is all non-negative numbers (x ≥ 0).

Likewise, for the function \(y=x^2\) no matter what the input is, the output is always non-negative, as the square of a number is never negative. We say that the range of this function is all non-negative numbers (y ≥ 0).

 

Until now, you knew the terms ‘odd’ and ‘even’ were associated with numbers. Now you will get to know that you can have ‘odd’ and ‘even’ functions (sounds pretty odd, we know 😉). We can discuss them on another day.

 

You will also learn about non-linear functions, such as – quadratic and cubic functions, as well as polynomial functions – in more depth.

 

Trigonometric Functions

My best guess is that like functions in general, you have also been exposed to the basic trigonometric functions like sine, cosine, tangent, cotangent, secant and cosecant in Stage 5.

 

You may have solved right triangles using these functions and their definitions, but did you know that you could use these functions to solve for the side lengths and angles of any triangle and not just right triangles? The law of sines and the law of cosines will help you do that.

 

To make it more interesting, you will learn how to find these trig ratios for any angle and not just for angles in the range from 0° to 90°.

 

And to make it even more interesting, you will learn how the sine, and cosine (and the rest of the trig functions) of certain angles can even be negative! What? Weren’t they defined as the ratios of side lengths? Can side lengths of triangles even be negative? No, but the trig ratios can! Welcome to Stage 6 mate 😊

 

It’s impossible to explain how that can happen in a nutshell, but here’s something you will want to remember from now on:

• If an angle is between 0° and 90° inclusive, all six trig functions are positive.
• If an angle is between 90° and 180° inclusive, only sine and its reciprocal – cosecant – are positive.
• If an angle is between 180° and 270° inclusive, only tangent and its reciprocal – cotangent – are positive.
• Finally, if an angle is between 270° and 360° inclusive, only cosine and its reciprocal – secant – are positive.

You will also learn about some important trigonometric identities and how to solve trigonometric equations.

 

By the way, do you know the difference between an ‘equation’ and an ‘identity’? An equation works for one, two or some specific value(s) of the variable(s), whereas an identity works for all values of the variable(s). Let me show you a couple of simple examples.

 

4x = 8 is an equation because there’s only one value of x that fits in, and that’s 2. For no other value of x will 4x be equal to 8.

 

Now think about x + 2x = 3x: this is always true, no matter what the value of x is, right? This is an identity. This is an algebraic identity.

 

Likewise, we have trigonometric identities. The simplest one of those is, for any angle θ, \(sin^{2}\theta + cos^{2}\theta = 1\)

First, convince yourself that this always works. Choose any angle, find its sine on your calculator, square it and store the answer (or write it down). Do the same with the cosine of the angle. Add the two results. Do you get 1? You should. Any deviation from that answer is only a result of rounding the numbers you got.

 

How can you prove the above should always work? Hint: use a right triangle, name the sides a, b and c, and use the definitions of sine and cosine. Finally, use Pythagoras’ Theorem to simplify.

 

Calculus

Unlike the previous two topics, Calculus will be completely new (and fun!) to you. So, what exactly is Calculus all about? To understand that, first think about a linear function: y = mx + c

Any idea why this is called a linear function? Because if you plot this on a graph sheet, you get a straight line (line 🡪 linear).

 

The slope or the gradient of a linear relationship is constant and is equal to the value of the constant ‘m’ in the equation. It means that every time x increases by 1, y increases by m on that graph. If m < 0 it means that as x increases, y decreases. In other words, if the graph goes down as we move right, its slope is negative. But that’s still constant – it doesn’t keep changing from point to point on the graph.

 

Take for example the graph of the equation y = 2x + 1 The table below shows some values of x and the corresponding values of y:

x	0	1	2	3
y	1	3	5	7

 

Notice that every time x increases by 1, y increases by a fixed amount (2). This is called the slope of the line and is equal to the coefficient of x in the equation in its standard form.

 

The issue here is, not all equations will show up as a straight line when plotted on the coordinate plane. The slope of such graphs keeps changing from one point to another. Think about the parent quadratic function: \(y=x^2\). Let’s come up with a table of values as we did before:

x	0	1	2	3
y	0	1	4	9

 

Notice that when x goes up by 1 from 0 to 1, y goes up by 1 as well; but when x moves from 1 to 2, y goes up from 1 to 4 (a jump of 3); and when x increases from 2 to 3, y shoots up from 4 to 9 (an increase by 5). The slopes of such graphs are not fixed. They keep changing from point to point on the graph, as shown in the figure below.

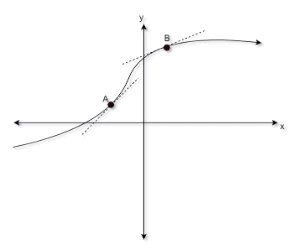
Notice how the slope at point A on the graph is steeper than at point B? To find the slope of such graphs (at any point you wish to), you need to use Calculus.

 

Calculus has a wide range of applications, particularly in engineering, science and technology. If you want to take up a career that requires a fair bit of knowledge in maths, you MUST be good at Calculus.

 

Exponential and Logarithmic Functions

You have learnt about exponents in Stage 5. You can think of logarithm as the ‘opposite’ of exponents. Let’s show you an example.

 

We know that \(2^3=8\)

 

Here’s another way to say the same thing: \(\log _{2} 8=3\) (read as “log base 2 of 8 equals 3”)

 

It’s so tempting to get confused, but don’t! It’s nothing more than another way to express the same relationship between the three numbers. Of course, that’s not all to it. There’s a lot more, but this is where it all starts from.

 

If there are laws of exponents (remember?), then there must be some laws of logarithms as well – after all, the two concepts go hand in hand.

 

Then there are exponential and logarithmic functions that you will learn about. Did you say, “is this function thing everywhere?” Indeed, it is! Algebraic, trigonometric, exponential, logarithmic – these are all different families of functions.

 

Oh, and any discussion on exponential and logarithmic functions, no matter how brief it is, is incomplete without a reference to a certain constant, called Euler’s number, denoted by the letter e. It’s an irrational number, discovered by a Swiss mathematician named Leonhard Euler. Its value is 2.7182818….

 

Euler’s number is not just another irrational number that your teacher will want you to memorise. It’s got a role to play in nature and our daily lives. For example, think about a situation in which the population of bacteria in a certain colony grows at a certain rate continuously over a period of time. ‘Continuously’ here means at every moment – every second, millisecond, microsecond, nanosecond, and so on…. If you want to find out the total number of bacteria after a long period, you need e! If you want to know more about e, check this video out.

 

Let’s talk about the last topic that you would come across in your HSC Year 11 Advanced Maths curriculum.

 

Statistical Analysis

This area is largely about probability and statistics. Again, you should have learnt the basics of this topic in Stage 5. The idea here is to build on that basic knowledge. You will learn about conditional probability, independent events, discrete random variables, solving probability problems using Venn Diagrams, mean or expected value, variance, standard deviation, etc.

 

It’s hard to tell you about each one of these in-depth, but let me bring up something interesting: if you roll a die, do you know the number you would be expecting? It’s the sum of each of the numbers that can show up multiplied by their respective probabilities. In this case, the mean or expected value equals

\(1\times \frac{1}{6}+2\times \frac{1}{6}+3\times \frac{1}{6}+4\times \frac{1}{6}+5\times \frac{1}{6}+6\times \frac{1}{6}\) which equals 3.5

 

W-H-A-T? Are you then expected to roll a 3.5? Haha! Not really. It means that if you were to roll the die a large number of times, record the results and take their mean or average, you would get closer and closer to 3.5

 

Conclusion and final tips

 

Year 12 builds on Year 11. Therefore, you should not take year 11 lightly. Let’s be honest, there’s a lot of information to be absorbed. But if you have a clear understanding of the fundamentals, study smart, take notes and find time to revise them, there’s no reason to be worried. To avail of our year 11 maths advanced tutoring, contact us today!